Um_nik: Stop learning useless algorithms, go and solve some problems, learn how to use binary search!

1、基本概述

二分算法的基本用法是在一个单调有序的集合或函数中查找一个解。因此，当问题的答案具有单调性时，可以考虑将问题的解，通过二分，转化为某种判定问题。每次分成左右两个区间，通过判断调整上下界，即继续搜索左区间还是右区间，直到找到目标元素。

更进一步的说，还可以扩展到三分算法取解决峰值函数的极值问题。三分算法将区间分成 3 个部分，可以明确判断答案不在哪一部分，舍弃三分之一的空间，继续进行查找。

此外，还有浮点数上的二分，其与整数二分大同小异。

总结一下，一般初学者在练习时可能会碰到以下问题：

• 整数集上的二分，需要注意左右区间的开闭情况，避免漏掉答案或者死循环；
• 实数域上的二分，需要注意精度问题。

二分的实现方法灵活多样，主要是处理边界上的差异时需要仔细考虑。为了避免混淆写法，下面只着重介绍一种实现方法。

2、算法实现

2.1、整数集上的二分

本文介绍的写法保证答案在 区间内，且当 时，循环退出，每次的二分中值 只属于左右区间的其中之一。

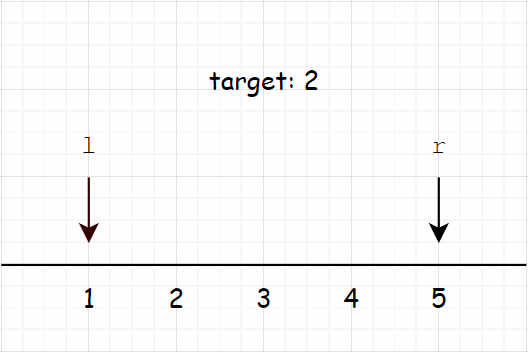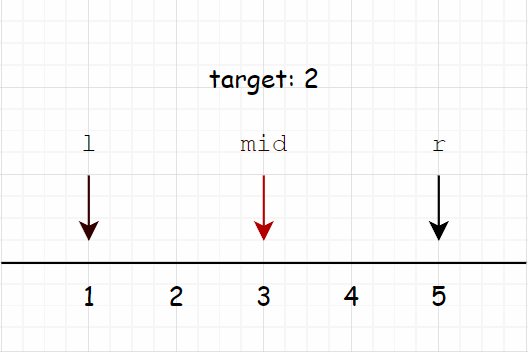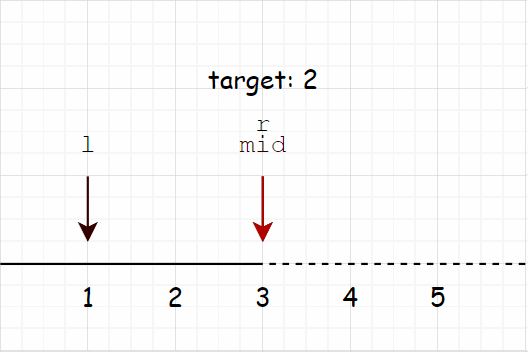
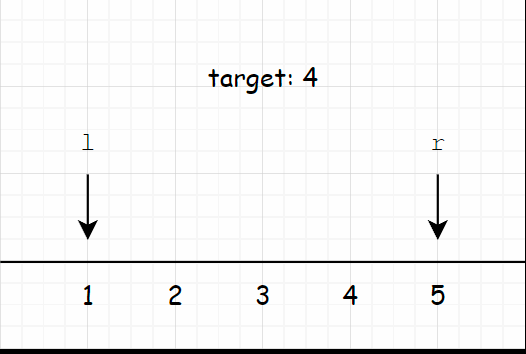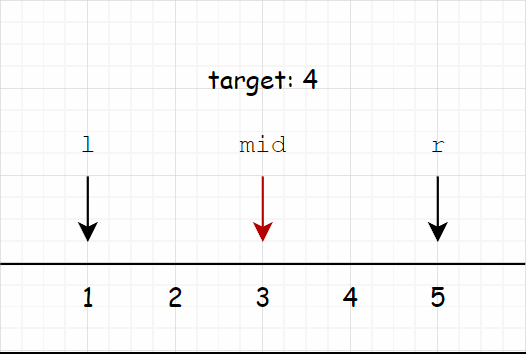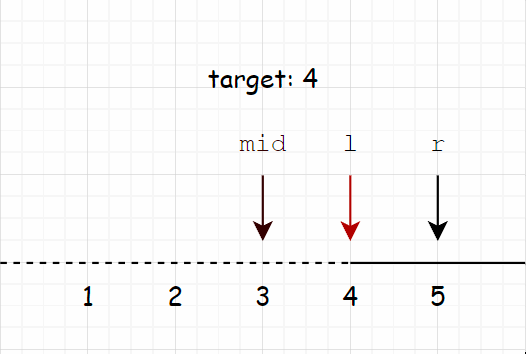
举个例子，比如我们要查找区间中最小的大于等于 的元素（即结果是 或 的后继）：

1
2
3
4
5
6
7
8

while (l < r) {
    mid = (l + r) / 2;
    if (a[mid] >= x) {
        r = mid;
    } else {
        l = mid + 1;
    }
}

首先，若 ，根据单调性，则在 后的元素比 更大。所以我们下一次查找的是左半段，即缩小上界 ；如果相等时，和上面的情况相同，下一次要查找的也是左半段，故合并在一起写成 ，因为要保证答案始终在区间内， 此时可能是解，所以 ，让边界取到 。

若 ，可知此时 一定不是我们的解，故 ，抛弃左半段。

相信上面的解释已经让你有些了解二分的基本思路。下面再举一个例子，在不降序列中查找小于等于 的最大的一个（即结果是 或 的前驱）：

1
2
3
4
5
6
7
8

while (l < r) {
	mid = (l + r + 1) / 2;
    if (a[mid] <= x) {
        l = mid;
    } else {
        r = mid - 1;
    }
}

尝试按照上面的步骤，自己解释一下上述代码。

可见这个二分写法有两种形式：

1. ，对于中间值，有 ；
2. ，对于中间值，有 。

为什么要区分 的形式呢？

主要是因为要避免死循环。假如让形式2为 ，那么当 与 相邻时，就有 ，若接下来进入 分支，就会造成死循环；若进入 这个分支，则循环退出时 ，答案不在区间内。所以这样区分是有必要的。

这种写法比较灵活，其好处是循环退出的条件是 ，也就是不用考虑最后的答案到底是在左端点还是右端点。

为了进一步加深理解，我们观察这两种形式，不难发现：主要是查找到两个相邻的两个值时，先去判断左端点还是右端点，前者先判断的是左端点，后者先判断的是右端点。所以我们可以利用这个特点，来决定具体采用那哪种形式。

例如，如果我们要找的是最大的一个解，那么在二分查找的过程中，区间会不断缩小，直至两个端点相邻。此时，先去判断较大的那个端点 ，如果 不满足条件，就让 ，也就是说排除这个右端点，否则就让 。如果要找的是最小的一个解也是同理。

此外，我们也可以利用这一特点，发现：形式1不会取到 ，形式2不会取到 。因此，我们可以扩展原来的区间 到 和 。扩大边界的好处是：如果目标不在我们查找的区间中，则最后位置一定在我们额外扩充的边界上，此时说明区间内不存在解。

总结一下吧，这种写法的基本流程是：

1. 通过分析问题，确定对于 mid，下一次要查找的是左半段还是右半段，以及 mid 保留在哪一个半段；
2. 根据分析结果，确定 mid 是用哪种形式，相邻时先判断右端点还是左端点；
3. 循环退出的条件是 ，所以最后答案任意输出其中一个即可。

这里提一下 C++ STL 中的两个函数 upper_bound 和 lower_bound，分别是查找第一个大于 的元素和第一个大于等于 的元素。

这里总结了以下情况：

1. 查找第一个大于 的元素的位置：upper_bound()。例如，pos = upper_bound(a, a + n, x) - a；
2. 查找第一个大于等于 的元素的位置：lower_bound()；
3. 查找第一个与 相等的元素：lower_bound() 且 ；
4. 查找最后一个与 相等的元素：upper_bound() 的前一个且 ；
5. 查找最后一个小于等于 的元素：upper_bound() 的前一个；
6. 查找最后一个小于 的元素：lower_bound() 的前一个。

C++ API STL算法库参考文档

2.2、实数域上的二分

也叫浮点二分，与整数集上的二分的写法大同小异，主要考虑精度问题。一般题目会给出保留小数位数或误差范围 。定义一个 EPS 常量为 1e-12（具体根据题目设置），循环退出的条件由原来的 改为 ， 不区分形式，只有 。

1
2
3
4
5

while (l + eps < r) {
     mid = (l + r) / 2;
     if (check(mid)) l = mid;
     else r = mid;
 }

此外，还有种固定循环次数的写法，不过这种写法一般不太会用到，主要是针对有些题目精度没有明确给出时使用：

1
2
3
4
5

 for (int i = 0; i < 100; i++) {
     mid = (l + r) / 2;
     if (check(mid)) l = mid;
     else r = mid;
 }

2.3、三分求凸性函数极值

凸性函数即在区间内是单峰函数，有唯一的极大值或极小值点（只能选其一）。

实现的思路是：对于一个开口向下的函数 ,在定义域 内，取两个点 和 ，从而将整个函数分成了三段。

1. 如果 ，则 和 同时在极大值的左侧，或是一个在左一个在右。无论是哪种情况，一定是在极大值的左侧，所以让 ；
2. 如果 ，则 和 同时在极大值的右侧，或是一个在左一个在右。无论是哪种情况， 一定是在极大值的右侧，所以让 ；
3. 通过上述的两个过程，区间不断往极大值逼近，最终求的解。

1
2
3
4
5
6

 while (l + eps < r) {
     lmid = l + (r - l) / 3.0;
     rmid = r - (r - l) / 3.0；
     if (f(lmid) < f(rmid)) l = lmid;
     else r = rmid;
 }

3、例题讲解

3.1、整数集上的二分

3.1.1、寻找指定和的整数对

问题描述

输入 个整数，找出其中的两个数，它们的和等于 。

题解

采用暴力的做法是用嵌套循环，枚举出所有的情况，时间复杂度为 。

采用二分算法优化查找。首先要确保序列的单调性，所以对数组进行排序。在查找的过程中，假设当前的数字是 ，查找在该数字后是否存在一个数字的值是 即可。因为数组是单调的，所以可以用二分优化查找第一个等于 的值。排序直接用 STL 中的 sort 函数，所以最后整个算法的复杂度是 。

练习：P1102 A-B 数对 - 洛谷(luogu.com.cn)

3.2、实数集上的二分

3.2.1、小车问题

问题描述

两人一车，人比车快，求它们从 A 到 B 的最短时间。

题解

假设甲、乙两人甲先坐车，乙走路。

不难想到最短的时间是两人同时出发，车先带甲到半路，然后让甲自己走到终点，车子再回去接乙，最终两人同时到达终点。此时花费的时间就是最少的时间。所以问题的关键是找到这个车子折返点。

简单分析一下，如果折返点距离起点越远，那么乙花费的时间就越长；如果折返点距离起点越近，那么甲花费的时间就越长。因此可以发现距离 与花费时间 有单调关系。因此可以用二分来解决。

具体做法是枚举 ，然后分别计算甲、乙到达终点的时间，如果甲先到达，那么就缩短其坐车的时间，即 ；否则就增加其坐车的时间，即 。最终计算出两者到达终点时间相同，就是最短的时间。时间复杂度为 。

练习：P1258 小车问题 - 洛谷 (luogu.com.cn)

3.3、二分答案

3.3.1、Balanced Stone Heaps

问题描述

有 堆石头，每堆石头有 个石头。你可以通过以下操作该改变每堆石头的数量：

• 从第 堆石头开始操作，直到第 堆石头；
• 假设当前是第 堆石头，可以选择 个石头移到第 堆，同时 个石头移到第 堆，所以如果这样操作之后，第 堆减少了 个石头。
• 每次操作 满足 。

求操作之后最少石头的那堆的最大值。

题解

对最小高度二分。对于当前假设的高度 ，每次操作的时候，采取贪心策略，倒序枚举，把当前的石头数尽可能地放到前两堆。需要注意的是，当前堆石头数减少的数量一定是 或是 的正整数倍数。

练习：Problem - 1623C - Codeforces

3.4、三分

3.4.1、Error Curves

问题描述

定义 ，其中 是二次函数，你需要找出最大的二次函数的最小值。

题解

二次函数在定义域内找出极值用三分即可。然后再取最大值。

练习：Problem - 3714 (hdu.edu.cn)

4、习题推荐

1. Problem - 1443C - Codeforces
2. Problem - 1408C - Codeforces
3. Problem - 626C - Codeforces
4. Problem - 371C - Codeforces
5. Problem - 2899 (hdu.edu.cn)
6. Problem - 4004 (hdu.edu.cn)
7. Problem - 2289 (hdu.edu.cn)
8. Problem - A - Codeforces
9. Problem - 1486D - Codeforces
10. Problem - 1119D - Codeforces
11. Problem - 1199C - Codeforces
12. Problem - 1041D - Codeforces
13. Problem - 1370D - Codeforces
14. Problem - 1260D - Codeforces