Codeforces Round 981 (Div.3)【A-F题解】

A. Sakurako and Kosuke

思维题

题意

初始位置 ，每次可移动 个单位。如果范围超过 ，则无法移动。

题解

观察位置序列 ，因此只需要判断 的奇偶性即可。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

void solve() {
  int n;
  cin >> n;
  cout << (n % 2 ? "Kosuke" : "Sakurako") << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：。
  • 空间复杂度：。

B. Sakurako and Water

模拟

题意

每次可以选择一条主对角线的所有值加 ，求使得所有的元素大于等于 的最小操作次数。

题解

显然，如果一条主对角线上的所有值大于等于 则不需要对其做任何操作，否则就找出这条主对角线上的最小值。答案为这些最小值之和。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

void solve() {
  int n;
  cin >> n;

  int ans = 0;
  vector<vector<int> > a(n, vector<int>(n));
  for (int i = 0; i < n; i++) {
    for (int j = 0; j < n; j++) {
      cin >> a[i][j];
    }
  }

  for (int k = 0; k < n; k++) {
    int mn = a[k][0];
    for (int i = k, j = 0; i < n && j < n; i++, j++) {
      mn = min(mn, a[i][j]);
    }
    ans += mn > 0 ? 0 : abs(mn);
  }

  for (int k = 1; k < n; k++) {
    int mn = a[0][k];
    for (int i = 0, j = k; i < n && j < n; i++, j++) {
      mn = min(a[i][j], mn);
    }
    ans += mn > 0 ? 0 : abs(mn);
  }

  cout << ans << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：，其中 是矩阵的大小。
  • 空间复杂度：。

C. Sakurako’s Field Trip

贪心

题意

定义一个数组 的价值是 的个数。元素可与对称元素进行交换，即 可与 交换，求数组的最小价值。

题解

计算交换前后的值，如果能使得价值变小，则更新价值。

对于 和 ，考虑与“内侧”元素的相等情况。

  • 交换前：判断 和 ；
  • 交换后：判断 和 。

Q&A

为什么不用判断“外侧”的情况？

在遍历数组的过程中，“外侧”情况已经判断过，不需要再重复判断。可以这么思考，如果“外侧”元素会影响本次交换，则应该在上一次进行过一次交换，如果再交换也只是还原，因此只需要考虑“内侧”元素的相等情况即可。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

void solve() {
  int n;
  cin >> n;

  vector<int> a(n);
  for (int i = 0; i < n; i++) {
    cin >> a[i];
  }

  int ans = 0;
  for (int i = 0; i < n - 1; i++) {
    ans += a[i] == a[i + 1];
  }

  for (int i = 0; i + 1 < n - 1 - (i + 1); i++) {
    int v = (a[i] == a[i + 1]) + (a[n - 1 - i] == a[n - 2 - i]);
    v -= (a[n - 2 - i] == a[i]) + (a[n - 1 - i] == a[i + 1]);
    ans -= max(v, 0);
  }

  cout << ans << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：，其中 是数组的大小。
  • 空间复杂度：。

D. Kousuke’s Assignment

集合

题意

给定数组 ，求其子串和为 的最大子串个数。

题解

根据贪思想如果当前子串的和为 ，则直接截断。在这种策略下，得到的数量一定是最多的。

用集合维护当前子串的和的情况，如果和为 ，则清空集合，也就是可以划分出新的一段区间和为 的子串。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

void solve() {
  int n;
  cin >> n;

  set<i64> ss;
  i64 sum = 0;
  int ans = 0;
  ss.insert(0);
  for (int i = 0, a; i < n; i++) {
    cin >> a;
    sum += a;
    if (ss.find(sum) != ss.end()) {
      ans++;
      sum = 0;
      ss.clear();
      ss.insert(0);
    } else {
      ss.insert(sum);
    }
  }
  cout << ans << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：，其中 是数组的大小。
  • 空间复杂度：，声明 ss 为区间和的集合，最坏情况是没有一个区间和为 的子串，在这种情况下集合的大小为 。

E. Sakurako, Kosuke, and the Permutation

图论 DFS

题意

给定一个排列 ，对于所有的元素 满足以下任一条件：

  • ；
  • ；

则认为这个排列是好的。

你可以交换任意两个元素，求最少的交换次数，使得排列符合上述条件。

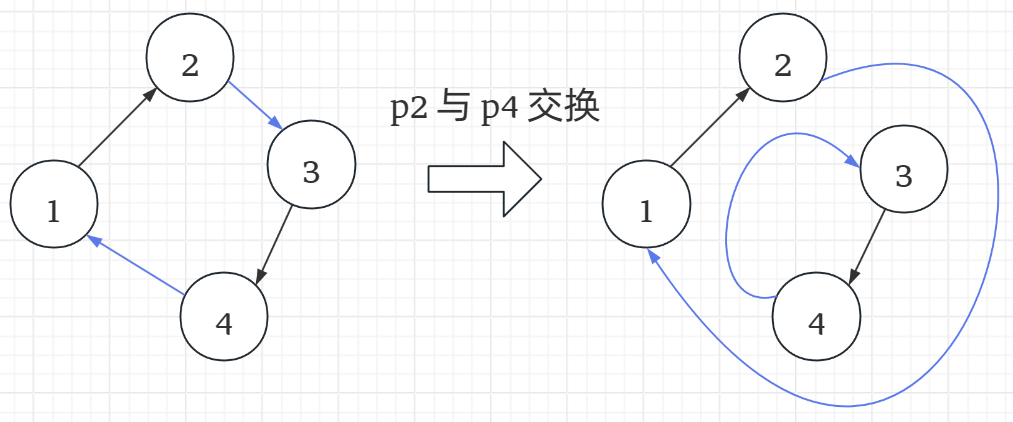
题解

从树的角度考虑，则题目中的条件可以看成：

  1. 节点的父节点是本身；
  2. 节点的父节点的父节点是本身。

交换操作就是将两个点的出边指向对应的节点。如 ，交换 指向原 指向点， 指向 指向原 指向的点，如下图所示。

因此从当前节点开始 DFS，直到当前节点的父节点就是本身。计算到目标节点经过的点数（包括目标节点），记 ，对答案的贡献是 。

另外，需要对搜索过的点进行标记。

Q&A

1. 为什么是 (cnt-1)/2？

cnt 其实代表了一条路径，这条路径一定是一个环。根据上述交换操作在图上的效果，要使的每个环中的节点个数不超过 ，这个次数显然就是 。

2. 为什么需要标记访问过的节点？

被访问过的点表示这个点在另外的环中，而一个点只能在一个环中。也就是已经计算过了，防止重复计算。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

void solve() {
  int n;
  cin >> n;

  vector<int> p(n);
  for (int i = 0; i < n; i++) {
    cin >> p[i], p[i]--;
  }

  int ans = 0;
  vector<bool> vis(n);
  for (int i = 0; i < n; i++) {
    if (!vis[i]) {
      int cnt = 0, x = i;
      do {
        vis[x] = true;
        x = p[x];
        cnt++;
      } while (x != i);
      ans += (cnt - 1) / 2;
    }
  }

  cout << ans << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：，其中 表示排列大小，保证每个点只被遍历一次。
  • 空间复杂度：，声明 vis 用于标记遍历过的点。

F. Kosuke’s Sloth

数论

题意

求斐波那契数列的长度，满足数列中有 个数能被 整除。

题解

有两个结论：

  1. 满足特定条件的递推式，模 后的序列一定具有周期性。
  2. 斐波那契数列，模 后的数列在周期内，也满足斐波那契数列的递推关系。

因此统计两个 的间隔，记 ，答案为 。

斐波那契数列模 的周期在数论中叫 皮萨诺周期。

两个结论的证明因为篇幅限制这里不做阐述了，请自行查阅相关资料或问 GPT。

参考代码

c++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
using i64 = long long;
using u64 = unsigned long long;
using u32 = unsigned;

constexpr int MOD = 1e9 + 7;

void solve() {
  i64 n;
  int k;
  cin >> n >> k;
  vector<int> a(3);
  a[0] = 1 % k, a[1] = 1 % k;

  int cnt = 1;
  while (a[0] != 0) {
    a[2] = (a[0] + a[1]) % k;
    a[0] = a[1];
    a[1] = a[2];
    cnt++;
  }

  cout << (n % MOD) * (cnt % MOD) % MOD << '\n';
}

int main(int argc, char * argv[])
{
  ios::sync_with_stdio(false);
  cin.tie(nullptr);

  int T;
  cin >> T;
  while (T--) {
    solve();
  }

  return 0;
}

复杂度分析

  • 时间复杂度：

    有皮萨诺周期 ，当 等号成立。 且我们只要找到第 个 的位置即可，因此时间复杂度可以认为是 。

  • 空间复杂度：。